Abstract

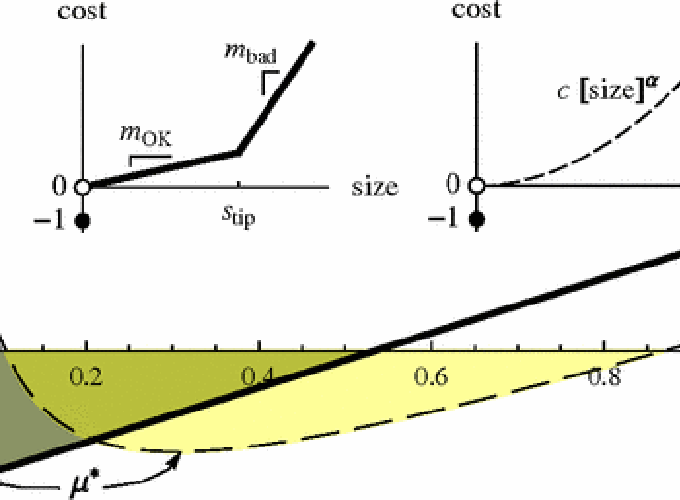
Controlling self-organizing systems is challenging because the system responds to the controller. Here, we develop a model that captures the essential self-organizing mechanisms of Bak-Tang-Wiesenfeld (BTW) sandpiles on networks, a self-organized critical (SOC) system. This model enables studying a simple control scheme that determines the frequency of cascades and that shapes systemic risk. We show that optimal strategies exist for generic cost functions and that controlling a subcritical system may drive it to criticality. This approach could enable controlling other self-organizing systems.