A search for the simplest chaotic partial differential equation
A search for the simplest chaotic partial differential equation
Abstract
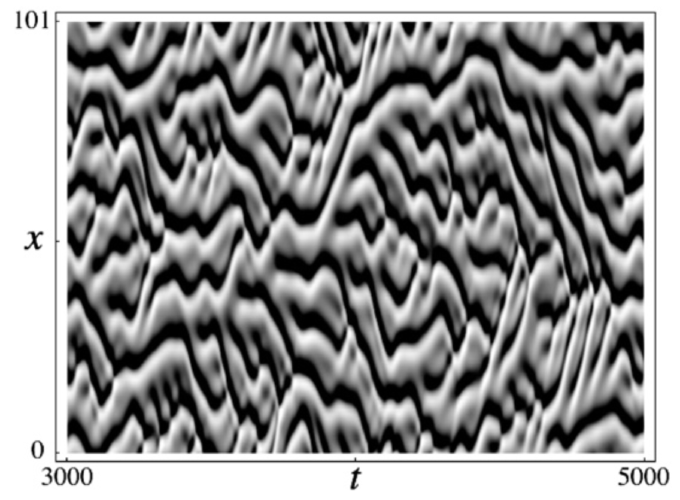
A numerical search for the simplest chaotic partial differential equation (PDE) suggests that the Kuramoto–Sivashinsky equation is the simplest chaotic PDE with a quadratic or cubic nonlinearity and periodic boundary conditions. We define the simplicity of an equation, enumerate all autonomous equations with a single quadratic or cubic nonlinearity that are simpler than the Kuramoto–Sivashinsky equation, and then test those equations for chaos, but none appear to be chaotic. However, the search finds several chaotic, ill-posed PDEs; the simplest of these, in the discrete approximation of finitely many, coupled ordinary differential equations (ODEs), is a strikingly simple, chaotic, circulant ODE system.
Type
Publication
Physics Letters A