Suppressing cascades of load in interdependent networks
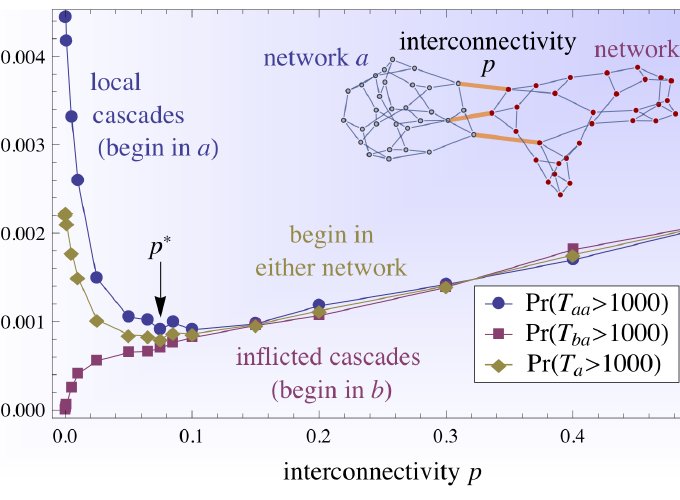 Figure from the Author Summary
Figure from the Author Summary
Suppressing cascades of load in interdependent networks
Abstract
Understanding how interdependence among systems affects cascading behaviors is increasingly important across many fields of science and engineering. Inspired by cascades of load shedding in coupled electric grids and other infrastructure, we study the Bak–Tang–Wiesenfeld sandpile model on modular random graphs and on graphs based on actual, interdependent power grids. Starting from two isolated networks, adding some connectivity between them is beneficial, for it suppresses the largest cascades in each system. Too much interconnectivity, however, becomes detrimental for two reasons. First, interconnections open pathways for neighboring networks to inflict large cascades. Second, as in real infrastructure, new interconnections increase capacity and total possible load, which fuels even larger cascades. Using a multitype branching process and simulations we show these effects and estimate the optimal level of interconnectivity that balances their trade-offs. Such equilibria could allow, for example, power grid owners to minimize the largest cascades in their grid. We also show that asymmetric capacity among interdependent networks affects the optimal connectivity that each prefers and may lead to an arms race for greater capacity. Our multitype branching process framework provides building blocks for better prediction of cascading processes on modular random graphs and on multitype networks in general.